|
|
ISSN: 2959-6513 - ISSN-L: 2959-6513 Volumen 4. No. 8 / Julio – diciembre 2024 Páginas 102 – 120
|
Métodos lúdicos entre pares para el aprendizaje de las matemáticas en segundo grado de básica
Playful methods among peers for learning mathematics in second grade of basic education
Métodos lúdicos entre pares para a aprendizagem da matemática na segunda classe do ensino básico
|
Dayana Evelyn Fritas Quispe https://orcid.org/0000-0002-0139-5679 Universidad César Vallejo. Lima, Perú |
Blanca Luz Unda Condezo https://orcid.org/0000-0002-5994-8600 Universidad César Vallejo. Lima, Perú |
Jhon Holguin-Alvarez https://orcid.org/0000-0001-5786-0763 Universidad César Vallejo. Lima, Perú |
http://doi.org/10.59659/revistatribunal.v4i8.48
Artículo recibido 15 de abril de 2024 / Arbitrado 28 de abril de 2024 / Aceptado 16 de junio 2024 / Publicado 01 de julio de 2024
Resumen
El aprendizaje de las matemáticas desarrolla el pensamiento lógico, analítico y la capacidad de abstracción, preparando a los estudiantes para los desafíos de un mundo cada vez más tecnológico. La presente investigación tuvo como objetivo evaluar la eficacia de la metodología lúdica entre pares para el aprendizaje de las matemáticas en estudiantes de segundo grado de primaria de una institución educativa en San Martín de Porres, Perú. El diseño pre experimental, aplicado a una muestra de 30 estudiantes de 7 a 9 años, utilizó una técnica de evaluación para medir las dimensiones del aprendizaje del pensamiento numérico, geométrico y algebraico a través de 55 operaciones y problemas. Los resultados muestran un notable incremento en el nivel de aprendizaje en las dimensiones estudiadas. En conclusión, la metodología empleada mejoró la comprensión de las matemáticas y contribuyó al desarrollo de habilidades y competencias matemáticas y de comunicación más sólidas en los estudiantes.
Palabras clave: Aprendizaje de las matemáticas; aprendizaje entre pares; ambiente colaborativo; metodología lúdica.
Abstract
Mathematics learning develops logical and analytical thinking and the ability to abstract, preparing students for the challenges of an increasingly technological world. The present research aimed to evaluate the effectiveness of the playful peer-to-peer methodology for learning mathematics in second grade students of an educational institution in San Martín de Porres, Peru. The pre-experimental design, applied to a sample of 30 students aged 7 to 9 years, used an assessment technique to measure the dimensions of learning numerical, geometric and algebraic thinking through 55 operations and problems. The results show a notable increase in the level of learning in the dimensions studied. In conclusion, the methodology used improved the understanding of mathematics and contributed to the development of stronger mathematical and communication skills and competencies in students.
Keywords: mathematics learning; peer learning; collaborative environment; playful methodology.
Resumo
Aprender matemática desenvolve o pensamento lógico, analítico e a capacidade de abstração, preparando os alunos para os desafios de um mundo cada vez mais tecnológico. O objetivo desta investigação foi avaliar a eficácia da metodologia lúdica peer-to-peer para a aprendizagem da matemática em alunos do segundo ano do ensino básico de uma instituição de ensino em San Martín de Porres, Peru. O desenho pré-experimental, aplicado a uma amostra de 30 alunos dos 7 aos 9 anos, utilizou uma técnica de avaliação para medir as dimensões da aprendizagem do pensamento numérico, geométrico e algébrico através de 55 operações e problemas. Os resultados mostram um aumento notável do nível de aprendizagem nas dimensões estudadas. Em conclusão, a metodologia utilizada melhorou a compreensão da matemática e contribuiu para o desenvolvimento de capacidades e competências matemáticas e de comunicação mais fortes nos alunos.
Palavras-chave: Aprendizagem da matemática; aprendizagem entre pares; ambiente colaborativo; metodologia lúdica.
INTRODUCCIÓN
Las matemáticas juegan un papel importante, tanto en la sociedad como en la vida cotidiana de cada uno de los niños y las niñas de educación básica, su enseñanza proporciona diferentes formas de ver, crear, establecer, construir, procesar y resolver problemas matemáticos; al desarrollar las competencias matemáticas se adquiere la capacidad para identificar y entender la función que desempeñan en la vida diaria, formando un alumno constructivista y reflexivo.
Los ambientes de aprendizaje les permiten tener la capacidad de elevar sus conocimientos y las habilidades en la resolución de problemas, empleando distintas estrategias para obtener sus resultados. El juego también estimula la creatividad y ayuda al entendimiento de lo que le rodea, conociéndose mejor a sí mismos, mejorando la interacción con los demás a través de reglas de operación definidas (Domínguez et al., 2022).
Las matemáticas, por tanto, constituyen una parte central del plan de estudios en los sistemas educativos de todo el mundo, por lo que tiene un impacto significativo en el éxito y el futuro de los estudiantes (Alt, 2023; Salvatierra et al., 2024). Los investigadores creen que aprender matemáticas puede estar cargado de dificultades que pueden conducir a repetidas experiencias de fracaso, falta de motivación e incluso pasividad. Uno de los principales desafíos en la enseñanza de matemáticas es involucrar activamente a los estudiantes en la construcción de conocimientos a través de actividades basadas en problemas y una comprensión profunda, que evite el aprendizaje rutinario de procedimientos que inhiben la capacidad de los estudiantes para alcanzar el dominio deseado (Karamert y Kuyumcu, 2021). Para abordar este reto, en los últimos años, las escuelas y los sistemas educativos han tenido que integrar nuevas metodologías, estrategias y recursos de aprendizaje en la enseñanza en general y en los planes de estudio de matemáticas en particular.
El aprendizaje de las matemáticas no se centra solo en la retención de fórmulas, aplicar conceptos y herramientas, sino que implica desarrollar la capacidad de análisis de la información, uso estrategias diferenciadas, planificación y razonamiento, que pueden utilizar los estudiantes para resolver problemas de la vida diaria (Leocadio et al., 2024). Este logro de aprendizajes ocurre mediante dos enfoques aplicados, el primero es conductual, se considera el cambio en la conducta, es decir, se aprende de lo más sencillo hasta llegar a lo más complejo. El segundo es cognitivo, lo cual significa el cambio de las estructuras mentales, es decir, a través de diversas estrategias, como la resolución de problemas y el aprendizaje in situ (Gabarda et al., 2022).
En este contexto, se ha sugerido emplear la gamificación y las estrategias lúdicas para mejorar la motivación de los estudiantes y los resultados del aprendizaje (Durrani et al., 2022). La gamificación se refiere al uso de mecánicas y elementos de juego en un entorno ajeno al juego. Como herramienta educativa, la gamificación se utiliza para facilitar el aprendizaje; fomentar la motivación y el compromiso; mejorar la participación de los alumnos, la interactividad de las lecciones y estimularlos a ampliar sus conocimientos (Jagušt et al., 2018).
Las actividades lúdicas se han convertido en una estrategia relevante a nivel mundial para mejorar el proceso de enseñanza-aprendizaje de las matemáticas. Según Ludeña y Zambrano (2022), la ludificación o estrategias lúdicas implican la integración de elementos de juego en contextos educativos con el objetivo de fomentar la participación, el compromiso y el aprendizaje significativo de los estudiantes. En este sentido, la ludificación se presenta como una herramienta poderosa para abordar la resolución de problemas matemáticos. Al crear ambientes de aprendizaje agradables y motivadores, las estrategias lúdicas estimulan el pensamiento crítico y la creatividad de los estudiantes (Vilaña et al., 2024).
Esto permite que los alumnos se involucren activamente en el proceso de aprendizaje, desarrollen habilidades de resolución de problemas y adquieran conocimientos matemáticos de una manera más efectiva y duradera. Además, la ludificación en la enseñanza de las matemáticas puede ayudar a reducir la ansiedad y la aversión que algunos estudiantes pueden sentir hacia esta asignatura. Al presentar los conceptos matemáticos de una manera más lúdica y atractiva, se puede fomentar una actitud más positiva y una mayor confianza en las propias capacidades de los alumnos.
La metodología lúdica entre pares es un método de enseñanza de juegos de aprendizaje donde los estudiantes mejoran sus habilidades matemáticas y participan activamente resolviendo problemas y apoyándose mutuamente (Segundo et al., 2022). Las bases teóricas, resaltan que las técnicas y estrategias didácticas lúdicas influyen en los estudiantes, debido a que interactúan en la adquisición, construcción o estructuración de la información que está almacenada previamente. Para Yanchapaxi et al. (2024), también fomenta el hábito de reflexionar y de interpretar problemas, fortaleciendo su proceso de aprendizaje. Con el juego entre pares se motiva el estudio y el análisis, se promueve el aprendizaje significativo, se refinan las tácticas y estrategias funcionales, y en general, se fomenta una actitud colaborativa al enfrentarse, en equipo, a situaciones problémicas.
Según Berlinski et al. (2023) y Hu et al. (2023), las actividades entre pares fomentan la interacción en el aula, aumentan el rendimiento académico y promueven habilidades cognitivas y sociales superiores al trabajo individual. Investigaciones actuales demuestran que la intervención temprana de los docentes en la observación de dificultades en el aprendizaje de las matemáticas, junto con estrategias de resolución de problemas y enseñanza basada en interacciones entre pares, promueven el desarrollo metacognitivo y el éxito en el aprendizaje (Aydın y Dinçer, 2022; Yu y Schunn, 2023). De igual modo, Aunio et al. (2021) y Qiu et al. (2023), consideran que la enseñanza entre pares promueve el rendimiento escolar, efectiviza y fomenta la motivación, colaboración y comprensión rápida (Aunios et al., 2021; Qiu et al., 2023).
Según el Ministerio de Educación (2023b) de Perú, en primaria, solo el 11,2 % de los alumnos de 2° grado alcanzaron el nivel satisfactorio en Matemática. La Red de Estudios para el Desarrollo advirtió que no se han observado avances significativos en el sistema educativo. Las principales preguntas de investigación exploradas en este estudio fueron: a) ¿Las actividades de gamificación inciden en los niveles de desempeño de los estudiantes de tercer año de EGB?; y b) ¿La gamificación modifica la actitud de los estudiantes hacia las clases de matemáticas? Solo el 6,7 % de la región selva logró un nivel satisfactorio. En 2023, la medida promedio se mantiene estable, sin diferencias estadísticamente significativas, en comparación con la de 2022. Asimismo, esta medida se ubica en el punto de corte que separa el nivel En proceso del nivel En inicio (Ministerio de Educación, 2023a).
Según este informe, en Matemática, el principal desafío es movilizar a los estudiantes de los niveles En inicio y Previo al inicio hacia niveles superiores. En los diferentes estratos, la medida promedio se encuentra cercana al punto que marca el comienzo del nivel En proceso y lejana al nivel Satisfactorio. Esto indica la existencia de rezagos en los aprendizajes, especialmente de los estudiantes del área rural.
Teniendo en cuenta este contexto, es necesario cuestionarse ¿cuáles son los efectos de una metodología lúdica basada en trabajo entre pares para mejorar el nivel de aprendizaje en matemática? El objetivo, por tanto, de la presente investigación fue evaluar la eficacia de la metodología lúdica entre pares en el aprendizaje de las matemáticas en estudiantes de segundo grado de primaria de una institución educativa en San Martín de Porres, Perú.
MÉTODO
La investigación es transversal, de tipo cuantitativo, con un diseño pre experimental, con mediciones pre y post test realizadas dos meses antes y después de la intervención. La muestra se conformó con 30 estudiantes del segundo grado del nivel primario de una Institución Educativa del distrito de San Martín de Porres, el 20% representado por el género masculino y el 80% el femenino. El rango de edad se ubicó entre 7 y 9 años. El muestreo fue no probabilístico clase única, debido a que la población estaba definida y limitada.
En cuanto a los criterios de selección se incluyeron todos los estudiantes que cursan el período lectivo 2024 y se excluyeron los que presentaron más del 30% de inasistencia a la actividad experimental.
Se aplicó una técnica de evaluación para valorar las dimensiones del aprendizaje de las matemáticas, en tres dimensiones, pensamiento numérico, geométrico y algebraico; a través de 55 operaciones y problemas. Las respuestas fueron calificadas bajo el esquema dicotómico, acierto = 1; error = 0. La resolución se estableció en un formato de aplicación individual en un tiempo de 90 minutos. Se calculó el Alfa de Cronbach como se muestra en la tabla 1, lo que indica el grado de confiabilidad del instrumento.
Tabla 1. Operaciónalización de las variables.
|
Dimensiones |
Indicador: ítem (índice Alfa de Cronbach) |
|
1.Pensamiento numérico |
1.1 Realizar el cálculo mental: 1(0.847), 2(0.848), 3(0.846), 4(0.846), 5(0.847), 6(0.845) |
|
1.2 Realizar las soluciones de problemas de cantidad: 7(0.846), 8(0.849), 9(0.849), 10(0.846), 11(0.847), 12(0.848) |
|
|
1.3 Analizar de datos estadísticos: 13(0.846), 14(0.846), 15(0.847), 16(0.845) , 17(0.846), 18(0.849), 19(0.849) |
|
|
1.4 Ejecutar operaciones y comprobarlas: 20(0.846), 21(0.847), 22(0.848), 23(0.846), 24(0.846), 25(0.847)
|
|
|
2.Pensamiento geométrico |
2.1 Discriminar las figuras geométricas: 26(0.845), 27(0.846), 28(0.849), 29(0.849), 30(0.846), 31(0.847), 32(0.848) |
|
2.2 Reconocer las propiedades básicas de las figuras: 33(0.846), 34(0.846), 35(0.847), 36(0.846), 37(0.846), 38(0.849), 39(0.849) |
|
|
2.3 Identificar las relaciones espaciales: 40(0.846), 41(0.847), 42(0.848), 43(0.846), 44(0.846), 45(0.847), 46(0.845), 47(0.846) |
|
|
3.Pensamiento algebraico |
3.1 Equivalencias e igualdad: 48(0.849), 49(0.849), 50(0.846) |
|
3.2 Ecuaciones lineales: 51(0.846), 52(0.848), 53(0.846) |
|
|
3.3 Realizar la representación gráfica de fracciones: 54(0.846), 55(0.847), 56(0.845) |
En la investigación, la validación se realizó con la contribución de tres expertos versados en el tema, una maestra de grado y dos doctoras especialistas, utilizando el método de Juicio de Expertos. Para estimar la confiabilidad o consistencia interna de la prueba, se aplicó la prueba de Kuder Richardson, KR, ya que los ítems a evaluar son dicotómicos, obteniéndose un índice de KR-20 fue de 0,88, lo que permite considerar que el instrumento es confiable y que sus ítems reflejan adecuadamente las características muestrales de los sujetos intervenidos.
El reporte de la investigación estuvo avalado por el Comité de Ética de la Escuela Profesional de Educación Primaria de una universidad privada de Lima, CE/UCV-N°. 018, contribuyendo a la formación sólida, científica de manera ética, responsable y transparente.
Se utilizó una metodología didáctica basada en el aprendizaje entre pares, que promovió el intercambio y colaboración horizontal entre los estudiantes. Se aplicaron 20 actividades en ocho semanas consecutivas, cada una presentó una duración de 40 minutos, las cuales se realizaron dentro del aula. Estuvieron orientadas en mejorar el aprendizaje matemático entre pares, en sus tres dimensiones, utilizando materiales concretos como chapitas, figuras geométricas y bloques lógicos. Cada sesión se desarrolló con una estructura de tres momentos didácticos, inicio, desarrollo y cierre.
En la etapa de inicio, se motivó a los estudiantes mediante dinámicas de interacción, y se presentaron los objetivos esperados. En el desarrollo, se abordaron las tres dimensiones objeto de estudio a través de diferentes estrategias lúdicas. Finalmente, en el cierre se llevó a cabo la metacognición, donde los estudiantes reflexionaron sobre su aprendizaje y progreso. Se diseñaron estrategias de aprendizaje colaborativo, aprendizaje basado en problemas y enseñanza recíproca.
El pre test se llevó a cabo dos meses antes de ejecutar el programa, con 90 minutos de duración. Este sirvió como línea base para comparar los resultados posteriores. Se utilizó una prueba validada para evaluar las dimensiones definidas. Luego, se implementó la intervención, utilizando materiales concretos como herramienta principal entre pares. Después de dos meses se aplicó una evaluación post test para valorar el aprendizaje matemático después de la intervención.
RESULTADOS
El aprendizaje matemático de los estudiantes de segundo grado mejoró después de la aplicación de la metodología entre pares con el uso de materiales concretos. No se registró ningún alumno con nivel bajo, lo que significa que el programa de intervención incidió positivamente en el grupo estudiado. El nivel alto fue alcanzado por 29 alumnos, lo cual evidencia la efectividad del programa diseñado y de sus estrategias. La significancia representa el 0.000 de error, por lo cual, el p-valor es menor a 0.05, confirmando que esta mejora es estadísticamente significativa. Por ello, se respalda la afirmación de que la metodología entre pares con materiales didácticos influye de manera positiva y significativa en el aprendizaje matemática de los estudiantes (Tabla 2).
Tabla 2. Comparación con la prueba del Signo del nivel de aprendizaje de las matemáticas.
|
|
N |
Sig. |
|
Bajoa |
0 |
0.000 |
|
Altob |
29 |
|
|
Medioc |
1 |
|
|
Total |
30 |
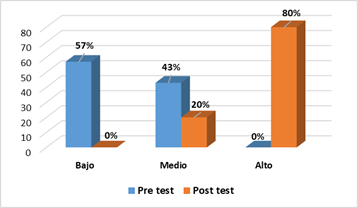
La figura 1 refleja la evolución en el aprendizaje matemático en la dimensión de pensamiento numérico, después de la metodología lúdica entre pares. Al inicio del estudio, el 57% se ubicaba en el nivel bajo de aprendizaje, asimismo se evidencia que ninguno poseía un nivel alto. Por otro lado, en la evaluación post test, se invierten los resultados, no se ubicaron estudiantes en el nivel bajo, el 20% se mantiene en el nivel medio y un notable 80% de los sujetos evaluados se ubican en el alto, aptos para rendir en las habilidades numéricas, después de aplicado el programa de aprendizaje matemático colaborativo.
Los alumnos de segundo grado resolvieron de forma eficiente problemas, realizaron cálculos mentales para resolver problemas y fueron capaces de crear nuevos ejercicios problémicos, interpretaron los datos para obtener información significativa y comprendieron conceptos básicos para la ejecución de operaciones matemáticas. Con 22 diferencias positivas se evidencia la mejora del grupo intervenido y una significancia bilateral de 0.000, lo que sustenta una influencia positiva y significativa de la metodología lúdica entre pares, confirmando la influencia beneficiosa en el pensamiento numérico.
Figura 1. Evaluaciones pre test y post test sobre el desarrollo del pensamiento numérico.
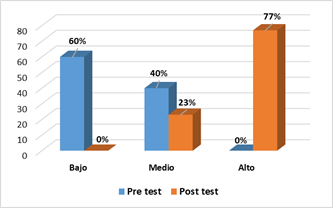
La figura 2 muestra que, al inicio del estudio, la mayoría de los estudiantes, el 60%, se ubican en el nivel bajo de aprendizaje matemático, ninguno ubicado en el nivel alto. Por otro lado, en la evaluación post test, se describe que el 23% se mantiene en el nivel medio y un notable 77% de los sujetos evaluados se ubican en el nivel alto, después de haber aplicado el programa de aprendizaje. Los alumnos del segundo grado reconocen de forma eficiente las características de las figuras geométricas y las relaciones espaciales de su entorno. No se registraron diferencias negativas, lo que significa que no se encontraron casos de disminución en el pensamiento geométrico después de la intervención. Con 25 diferencias positivas se representa la mejora del grupo intervenido y, una significancia bilateral de 0.000, permitiendo comprobar la influencia beneficiosa en el pensamiento geométrico.
Figura 2. Evaluaciones pre test y post test en el desarrollo del pensamiento geométrico
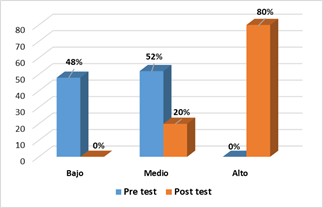
La figura 3 permite comprobar que antes de la intervención, el 48% de los sujetos se ubican en el nivel bajo de aprendizaje matemático en la dimensión algebraica, el 52%% estaban en un nivel medio y ninguno clasificaba en el nivel alto. En la evaluación post test, ningún estudiante se encuentra en el nivel bajo, el 20% se mantiene en el nivel medio y el 80% de los se ubicaron en el nivel alto, después de haber aplicado el programa de aprendizaje matemático colaborativo. Los alumnos del segundo grado calculan de forma eficaz las cantidades o expresiones numéricas distintas entre sí, identifican y resuelven las variables de la ecuación lineal en forma exacta y reconocen las partes de una fracción, logrando representar de forma gráfica.
En cuanto a la comprobación de hipótesis, se halló que el pensamiento algebraico de los estudiantes de segundo grado mejoro después de la aplicación de la metodología lúdica entre pares. No se detectaron casos de disminución en el pensamiento algebraico después de la intervención. Con 27 diferencias positivas representan la mejora del grupo intervenido y la significancia bilateral de 0.000, demostrando la significativa de la metodología lúdica entre pares.
Figura 3. Evaluaciones pre test y post test en el desarrollo del pensamiento algebraico
En la tabla 3 se muestran los resultados del análisis de varianza, ANOVA, de dos vías. No se encontraron diferencias significativas entre las tres dimensiones, pensamiento numérico, geométrico y algebraico, F(2, 12) = 0.000, p = 1.000, por lo que se puede afirmar que estas dimensiones tuvieron un comportamiento similar; ni se encontró una interacción significativa entre el tipo de pensamiento y el momento de la evaluación, F(2, 12) = 0.000, p = 1.000, lo que demuestra que los cambios en los puntajes de pensamiento numérico, geométrico y algebraico entre el pre test y el post test no dependen del tipo específico de pensamiento.
En otras palabras, si hubiera una interacción significativa, expresaría que el efecto del momento de la evaluación, sobre los puntajes de pensamiento, varía según el tipo de pensamiento.
Esto sugiere que los cambios en los puntajes de pensamiento entre el pre test y el post test son similares para los diferentes tipos de pensamiento. En resumen, la falta de interacción significativa implica que el efecto del momento de la evaluación sobre los puntajes de pensamiento no depende del tipo específico de pensamiento considerado. Los cambios en los puntajes de pensamiento numérico, geométrico y algebraico entre el pre test y el post test son consistentes y no varían significativamente según el tipo de pensamiento (Tabla 3).
Tabla 3. Análisis de varianza de dos vías con medidas repetidas para los puntajes de pensamiento numérico, geométrico y algebraico.
|
Source |
df |
sum_sq |
mean_sq |
F |
PR(>F) |
|
C(tipo_pensamiento) |
2.0 |
1.110223e-16 |
5.551115e-17 |
0.000000 |
1.000000 |
|
C(momento) |
1.0 |
1.110223e-16 |
1.110223e-16 |
0.000000 |
1.000000 |
|
C(tipo_pensamiento): C(momento) |
2.0 |
1.110223e-16 |
5.551115e-17 |
0.000000 |
1.000000 |
|
Residual |
12.0 |
1.110223e-16 |
9.251859e-18 |
NaN |
NaN |
Con estos resultados se comprueba que, la metodología didáctica basada en el aprendizaje entre pares es fundamental para el desarrollo del pensamiento numérico, geométrico y algebraico en niños de segundo grado. Al interactuar con sus compañeros, colaborar y participar en actividades lúdicas, los estudiantes tienen la oportunidad de explicar conceptos, resolver problemas y construir conocimiento de manera colaborativa. Esto fomenta una comprensión más profunda y significativa de las matemáticas. Además, el aprendizaje entre pares permite a los niños practicar habilidades de comunicación, argumentación y trabajo en equipo, esenciales para su desarrollo integral. Al aplicar esta metodología en las áreas de matemáticas, los docentes crearon un ambiente de aprendizaje activo, motivador y adaptado a las necesidades de cada estudiante.
DISCUSIÓN
Los resultados del pre test en la presente investigación, coinciden con los expuestos por Moreno et al. (2016), cuando plantea que el bajo nivel en matemáticas que exhiben los estudiantes de educación básica en Latinoamérica, es un problema que ha sido evidenciado sistemáticamente por numerosas pruebas internacionales estandarizadas. Una de ellas es el Programa para la Evaluación Internacional de Estudiantes, PISA, por sus siglas en inglés, las cuales son llevadas a cabo de forma trianual con el fin de medir los conocimientos y habilidades de estudiantes alrededor del mundo en matemáticas, ciencias y compresión lectora.
Así mismo, Farfán et al. (2022), consideran que, en la actualidad se ve con preocupante mirada los logros obtenidos por los estudiantes de la educación básica con respecto a su nivel de afianzamiento y dominio en el área de matemática, planteando que el sector educativo, fue, además, uno de los más perjudicados por la crisis producida a raíz de la pandemia COVID-19; que afectó seriamente el desarrollo de las competencias y capacidades matemáticas de los estudiantes, repercutiendo de manera objetiva en la adquisición de aspectos conceptuales elementales para poder enfrentar los grandes retos de la sociedad actual.
Los resultados significativamente superiores, obtenidos al aplicar la metodología lúdica por pares para la enseñanza de las matemáticas, se corresponden con los observados por Araya et al. (2022), quien considera que su investigación deja en evidencia un supuesto fundamental, desde un punto de vista pedagógico y neurocientífico, el uso de metodologías lúdicas resulta gravitante en el proceso de enseñanza-aprendizaje. Esta premisa radica en que el juego no solo es importante para el trabajo en el aula, sino que es imprescindible, pues jugar es inherente al ser humano, por lo que no se puede disociar del proceso educativo.
En atención a ello, se requiere una reflexión profunda respecto de su importancia y de las estrategias para su implementación. Las características sociocognitivas de los estudiantes de segundo ciclo básico, reafirman la importancia de introducir estas actividades para captar la atención y activar el proceso de motivación en el aula, por consiguiente, la labor docente consiste en abordar la planificación del proceso de enseñanza y aprendizaje desde un prisma que recurra a las herramientas imaginativas, lo que constituirá una excelente instancia para enriquecer el proceso educativo. La tarea, sin duda, se remitirá a lo didáctico y metodológico.
Por su parte, Quevedo (2023), dejó establecido que existen múltiples documentos con valor científico centrados en la forma exitosa de abordar el conocimiento matemático, que reconocen la importancia de tener en cuenta los soportes teóricos que respaldan los métodos y la didáctica que debe implementarse al momento de enseñar matemática. Los resultados alcanzados en el proceso de enseñanza de las matemáticas de los alumnos del ciclo básico en la escuela Fe y Alegría de Colombia, evidencian la necesidad de revisar, de manera permanente, las estrategias didácticas, con el fin incorporar elementos innovadores, considerando los contenidos básicos imprescindibles que exige el currículo vigente, para que sean comprendidos y llevarlos a la práctica en la cotidianidad familiar y escolar.
Finalmente, concluye que las técnicas lúdicas usadas en el mejoramiento de la enseñanza de las matemáticas en segundo grado se fundamentan en estrategias de participación, enmarcadas en una situación de juego, que exige la puesta en práctica del razonamiento lógico y el cálculo matemático. Estas actividades se diseñaron para resultar agradables, cortas y divertidas con normas que regulen el desarrollo del juego.
La presente investigación demuestra que la metodología lúdica por pares, apoya el trabajo colaborativo, lo que coincide con Calle et al. (2020), que utiliza estrategias metodológicas para el desarrollo de un pensamiento crítico en el área de las matemáticas y uno de ellos es el aprendizaje basado en problemas, mediante un trabajo en equipo, por pares, ya que contribuye a que el alumnos se mantenga activo, despierta la curiosidad por aprender, la creatividad para desarrollar diversas actividades y afianza el desarrollo crítico, facilitando la adquisición e interpretación de un problema matemático, siguiendo los pasos adecuados de la metodología con la ayuda de su par. Esto requiere que el docente se involucre en la práctica educativa para así conseguir resultados positivos en el desarrollo de habilidades y competencias adecuadas.
Se concuerda con Aristizábal y Colorado (2016), quienes realizaron una investigación experimental y exploratoria, que les permitió desarrollar distintas habilidades y relaciones para reforzar las operaciones numéricas básicas, de adición y sustracción, en estudiantes de básica en la Institución Educativa Henry Marín Granada en Colombia, bajo una estrategia didáctica mediada por el juego, que sirvió de ayuda al abordar las dificultades encontradas en las operaciones antes mencionadas, sus combinaciones y la resolución de problemas, la cual consistió en trabajar una serie de actividades y/o juegos los cuales generaron mayor motivación e interés en los estudiantes, lo que permitió ratificar que la enseñanza de las matemáticas mediadas por esta estrategia logra la transformación del proceso de enseñanza-aprendizaje.
La presente investigación se apoya y coincide en su diseño con los cinco procesos generales que se contemplaron en los Lineamientos Curriculares de Matemáticas, enunciados por Martínez et al. (1999), formular y resolver problemas; modelar procesos y fenómenos de la realidad; comunicar; razonar y comparar; ejercitar procedimientos y algoritmos. En los diferentes momentos vividos en el desarrollo de la estrategia se generaron espacios donde los estudiantes a través del juego pudieron acercarse a los algoritmos de las operaciones con números naturales, mejorando su habilidad en las tres dimensiones estudiadas.
Posteriormente, se trabajaron situaciones problemas cuya solución se buscaba a través de los juegos, identificando cuales operaciones debían tener en cuenta para encontrar dicha solución, lo que concuerda con la estrategia didáctica aplicada en el proyecto de Domínguez et al. (2022), quienes desarrollaron el pensamiento numérico a través del juego, en las cuatro operaciones básicas.
Por su parte, De Guzmán (1992), confirma en su investigación la clara relación con los cinco tipos de pensamiento matemático, enunciados en los Lineamientos curriculares, en la aritmética, el pensamiento numérico; en la geometría, el pensamiento espacial y el métrico; en el álgebra y el cálculo, el pensamiento métrico y el variacional, en la probabilidad y estadística, así como en el pensamiento aleatorio.
Se concuerda con Ramirezparis (2009), que considera a la metodología lúdica y el aprendizaje por pares como estrategias fundamentales en la enseñanza de las matemáticas, ya que fomentan un ambiente de aprendizaje más dinámico, interactivo y efectivo. El juego, como herramienta pedagógica, permite a los estudiantes desarrollar habilidades matemáticas de manera natural y divertida, estimulando su curiosidad y motivación. A través de actividades lúdicas, los estudiantes pueden explorar conceptos matemáticos, resolver problemas y practicar habilidades de una manera más relajada y menos intimidante que en un entorno tradicional de enseñanza.
Por otro lado, Jiménez y Mendoza (2022), consideran que el aprendizaje por pares promueve la colaboración y el intercambio de ideas entre los estudiantes, lo que enriquece el proceso de aprendizaje. Al trabajar en equipo, los estudiantes pueden explicar conceptos a sus compañeros, discutir estrategias de resolución de problemas y aprender de las perspectivas de otros. Esta interacción entre pares fomenta el desarrollo de habilidades sociales, la comunicación efectiva y la capacidad de trabajar en equipo. Además, la metodología lúdica y el aprendizaje por pares permiten a los docentes adaptar su enseñanza a las necesidades y estilos de aprendizaje individuales de los estudiantes. Al incorporar juegos y actividades interactivas en el aula, los docentes pueden abordar diferentes niveles de habilidad, ritmos de aprendizaje y preferencias de los estudiantes. Esto contribuye a crear un entorno de aprendizaje inclusivo y acogedor, donde todos los estudiantes tienen la oportunidad de participar y progresar a su propio ritmo.
Los juegos didácticos, utilizados como método, procedimiento y medio, según Bravo et al. (2020), facilitan la comprensión y uso de los contenidos matemáticos, favorecen el desarrollo del pensamiento lógico, y relacionan la matemática con situaciones generadoras de diversión, criterios que avalan los resultados obtenidos en la presente investigación. Además, Sánchez et al. (2023), añade que el trabajo en grupos y la interacción entre pares promueven el desarrollo de habilidades de colaboración, creatividad, razonamiento y autoestima en los estudiantes.
Jiménez y Mendoza (2022), abordan un aspecto esencial para alcanzar estas metas, al resaltar la importancia de capacitar a los docentes en el uso de estrategias lúdicas, coherentes con los contenidos impartidos, para consolidar el aprendizaje significativo de las matemáticas.
CONCLUSIONES
La aplicación de la metodología lúdica entre pares logró mejorar el nivel de aprendizaje de las matemáticas en los estudiantes de segundo grado de primaria del distrito de San Martín de Porres, de la ciudad de Lima, Perú, comprobado por el incremento que se obtuvo en las pruebas post test de las dimensiones de la variable aprendizaje de la matemática.
El estudio realizado corrobora la importancia del trabajo colaborativo, ya que los estudiantes aprenden de sus compañeros y se motivan mutuamente, desarrollando habilidades sociales y de comunicación. Por otro lado, al utilizar materiales concretos los estudiantes disfrutan del proceso de aprendizaje e interiorizan los conceptos numéricos de manera natural y divertida.
El uso de materiales ha potenciado significativamente la comprensión de figuras geométricas y la percepción de relaciones espaciales. Por otro lado, ha permitido a los estudiantes no solo identificar, sino también, aplicar conceptos geométricos de manera más profunda, debido al apoyo del docente para facilitar este proceso de aprendizaje; de manera similar se comporta el desarrollo del pensamiento algebraico y numérico en los estudiantes.
A través de la estrategia y la metodología utilizada, los estudiantes desarrollaron una comprensión más profunda y mejoraron su capacidad para resolver problemas, se logró fomentar el pensamiento crítico y aportar en otras variables emergentes, como las actitudes cooperativas, en un ambiente relajado, ya que los estudiantes debían trabajar juntos para alcanzar un objetivo común.
REFERENCIAS
Alt, D. (2023). Assessing the benefits of gamification in mathematics for student gameful experience and gaming motivation. Computers Education, 200, 104806. https://doi.org/10.1016/j.compedu.2023.104806
Araya, C. A., Molina, H. y Vargas, L. V. (2022). Impacto de metodologías lúdicas fundadas en las herramientas de la Educación Imaginativa en la motivación escolar de estudiantes de Segundo Ciclo Básico. Revista Realidad Educativa, 2(1), 88-116. https://doi.org/10.38123/rre.v2i1.199
Aristizábal, J. H. y Colorado, H. (2016). El juego como una estrategia didáctica para desarrollar el pensamiento numérico. Itinerario Educativo, 30(67), 123-137. https://doi.org/10.21500/01212753.2893
Aunio, P., Korhonen, J., Ragpot, L., Törmänen, M. y Henning, E. (2021). An early numeracy intervention for first-graders at risk for mathematical learning difficulties. Early Childhood Research Quarterly, 55, 252-262. https://doi.org/10.1016/j.ecresq.2020.12.002
Aydın, E. y Dinçer, Ç. (2022). “I did it wrong, but i know it”: Young children's metacognitive knowledge expressions during peer interactions in math activities. Thinking Skills Creativity, 45, 101104. https://doi.org/10.1016/j.tsc.2022.101104
Berlinski, S., Busso, M. y Giannola, M. (2023). Helping struggling students and benefiting all: Peer effects in primary education. Journal of Public Economics, 224, 104925. https://doi.org/10.1016/j.jpubeco.2023.104925
Bravo, S. d. l. C., Díaz, A. d. l. C. y Campos, E. (2020). Metodología para implementar la actividad lúdica en clases de Matemática en la secundaria básica cubana. EduSol, 20(73), 127-137. http://scielo.sld.cu/pdf/eds/v20n73/1729-8091-eds-20-73-127.pdf
Calle, Y. A., García, D. G., Mena, S. E. y Erazo, J. C. (2020). Aprendizaje basado en problemas y trabajo colaborativo para la enseñanza de Matemática. EPISTEME KOINONIA: Revista Electrónica de Ciencias de la Educación, Humanidades, Artes y Bellas Artes, 3(1), 436-458. https://dx.doi.org/10.35381/e.k.v3i1.1019
De Guzmán, M. (1992). Tendències innovadores en educació matemàtica. Butlletí de la Societat Catalana de Matemàtiques, 7, 7-34. https://revistes.iec.cat/index.php/BSCM/article/view/22058.001
Domínguez, S., Pérez, M. y Pérez, E. (2022). Ambientes de aprendizaje para favorecer competencias matemáticas en educación básica. Revista RedCA, 5(13), 144-162. https://revistaredca.uaemex.mx/article/view/18790/13905
Durrani, U. K., Al Naymat, G., Ayoubi, R. M., Kamal, M. M. y Hussain, H. (2022). Gamified flipped classroom versus traditional classroom learning: Which approach is more efficient in business education? The International Journal of Management Education, 20(1), 100595. https://doi.org/10.1016/j.ijme.2021.100595
Farfán, J. F., Lizandro, R., Rodríguez, D. B., Calderon, M. E. y Farfán, D. E. (2022). Estrategia khan academy en el aprendizaje de la matemática en la educación básica: una revisión teórica. Ciencia Latina Revista Científica Multidisciplinar, 6(6), 6871-6887. https://doi.org/10.37811/cl_rcm.v6i6.3926
Gabarda, V., Colomo, E., Ruiz, J. y Cívico, A. (2022). El aprendizaje de las matemáticas mediante tecnología en Europa: revisión de literatura. Texto Livre, 15, e40275. https://doi.org/10.35699/1983-3652.2022.40275
Hu, L., Chen, G. y Wu, J. (2023). Teaching talk for thinking: The efficacy of a peer talk teaching program for improving group thinking. Thinking Skills Creativity, 48, 101291. https://doi.org/10.1016/j.tsc.2023.101291
Jagušt, T., Botički, I. y So, H.-J. (2018). Examining competitive, collaborative and adaptive gamification in young learners' math learning. Computers Education, 125, 444-457. https://doi.org/10.1016/j.compedu.2018.06.022
Jiménez, L. y Mendoza, F. (2022). El juego como alternativa para la enseñanza de la matemática. Orkopata. Revista de Lingüística, Literatura y Arte, 1(1), 89-106. https://doi.org/10.35622/j.ro.2022.01.005
Karamert, Ö. y Kuyumcu, A. (2021). The effect of gamification on young mathematics learners’ achievements and attitudes. ournal of Educational Technology Online Learning, 4(2), 96-114. https://doi.org/10.31681/jetol.904704
Leocadio, P., Quintana, A. y Buden, I. d. l. C. (2024). El proceso de enseñanza-aprendizaje de las Matemáticas en la Universidad Autónoma de Santo Domingo. Desafíos. Varona, Revista Científico-Metodológica, 79, 1-22. http://scielo.sld.cu/pdf/vrcm/n79/1992-8238-vrcm-79-e2335.pdf
Ludeña, J. E. y Zambrano, J. M. (2022). Guía de actividades lúdicas para el desarrollo del pensamiento lógico-matemático en niños de Educación Inicial. Revista estudios del desarrollo social: Cuba y América Latina, 10(3). http://scielo.sld.cu/pdf/reds/v10n3/2308-0132-reds-10-03-e32.pdf
Martínez, A., Acero, C. A., Acevedo, D. C., Acevedo, M. P., Acevedo, C. J. y Acosta, G. L. (1999). Lineamientos curriculares: Matemáticas. MEN.
Ministerio de Educación. (2023a). Evaluación Nacional de Logros de Aprendizaje 2023. Resultados de aprendizaje. (pp. 1-114). Lima, Perú: MINEDU.
Ministerio de Educación. (2023b). Informe de Minedu sobre el nivel satisfactorio en Matemáticas. Perú: MINEDU.
Moreno, J., Piedrahita, A. A. y Rosecler, M. (2016). El rol del juego digital en el aprendizaje de las matemáticas: experiencia conjunta en escuelas de básica primaria en Colombia y Brasil. Revista electrónica de investigación en educación en ciencias, 11(2), 39-51. http://www.scielo.org.ar/pdf/reiec/v11n2/v11n2a04.pdf
Qiu, C., Long, B., Yu, D. y Cheong, K. H. (2023). Evolving the classroom: A mathematical and didactic exploration of teacher-guided peer learning. Chaos, Solitons Fractals, 174, 113853. https://doi.org/10.1016/j.chaos.2023.113853
Quevedo, J. L. (2023). La enseñanza de la matemática mediante la Lúdica en quinto grado de Educación Básica. Latam: revista latinoamericana de Ciencias Sociales y Humanidades, 4(2). https://doi.org/10.56712/latam.v4i2.849
Ramirezparis, X. (2009). La lúdica en el aprendizaje de las matemáticas. Zona próxima: revista del Instituto de Idiomas de la Universidad del Norte(10), 138-145. https://dialnet.unirioja.es/servlet/articulo?codigo=3220302
Salvatierra, J., Velasco, C., Vázquez, A. y Ortiz, W. (2024). La gamificación en el aprendizaje de las matemáticas en estudiantes de tercer grado de educación general básica de la unidad educativa Gloria Gorelik. Sinergia Académica, 7(Especial 3), 181-203. http://sinergiaacademica.com/index.php/sa/article/view/266/1100
Sánchez, J. L., Martínez, E. M., Poveda, V. I. y Castro, R. A. (2023). Técnicas lúdicas en la enseñanza-aprendizaje de matemáticas en estudiantes de séptimo grado, Cantón el Tambo, Ecuador. Revista Universidad y Sociedad, 15(5), 30-37. http://scielo.sld.cu/pdf/rus/v15n5/2218-3620-rus-15-05-30.pdf
Segundo, R., Merchán, A., López, V. y Daza, M. T. (2022). Development of executive functions in late childhood and the mediating role of cooperative learning: A longitudinal study. Cognitive Development, 63, 101219. https://doi.org/10.1016/j.cogdev.2022.101219
Vilaña, V. E., Villegas, M. A. E. y Ortiz, W. (2024). Sistema de tareas lúdicas para el desarrollo de habilidades en la resolución de problemas matemáticos en los estudiantes de sexto año de básica. Sinergia Académica, 7(Especial 4), 399-421. https://doi.org/10.51736/sa.v7iEspecial%204.314
Yanchapaxi, C. E., Fuentes, F. F., Córdova, L. M., Chicaiza, D. C. y Muñoz, L. M. (2024). Estrategia lúdica para desarrollar aprendizaje significativo en la asignatura de matemática. GADE: Revista Científica, 4(2), 192-211. https://revista.redgade.com/index.php/Gade/article/view/430
Yu, Q. y Schunn, C. D. (2023). Understanding the what and when of peer feedback benefits for performance and transfer. Computers in Human Behavior, 147, 107857. https://doi.org/10.1016/j.chb.2023.107857
