El estudio investigó si la implementación del modelo de sesiones de aprendizaje ARTE a través de Google Classroom mejora la competencia en resolución de problemas en estudiantes de Matemática Básica de una universidad en Lima. Esta investigación, de naturaleza cuantitativa, se enmarca en un enfoque aplicado y experimental. Aplicando los principios del aprendizaje experiencial de Kolb y el método Pólya, el modelo ARTE fue utilizado con un grupo de 48 estudiantes. Los resultados, analizados mediante pruebas no paramétricas debido a la distribución no normal de las calificaciones, revelaron mejoras significativas en todas las fases del método Pólya después de la intervención. Se deduce que el modelo ARTE tiene un impacto positivo en el desarrollo de la competencia en resolución de problemas.

Palabras clave: Competencia de resolución de problemas, Modelo ARTE, Ciclo de Kolb, Método Pólya, Google Classroom.

Abstract

The study investigated whether the implementation of the ART learning session model through Google Classroom improves problem-solving competence in Basic Mathematics students at a university in Lima. This research, of a quantitative nature, is part of an applied and experimental approach. Applying the principles of Kolb's experiential learning and the Pólya method, the ARTE model was used with a group of 48 students. The results, analyzed using non-parametric tests due to the non-normal distribution of the scores, revealed significant improvements in all phases of the Pólya method after the intervention. It is deduced that the ARTE model has a positive impact on the development of problem-solving competence.

Keywords: Self-esteem, Psychological well-being, Coping strategies, Women, Victims of violence.

Resumo

O estudo investigou se a implementação do modelo de sessão de aprendizagem ART através do Google Classroom melhora a competência de resolução de problemas em alunos de Matemática Básica de uma universidade em Lima. Esta pesquisa, de natureza quantitativa, insere-se numa abordagem aplicada e experimental. Aplicando os princípios da aprendizagem experiencial de Kolb e do método Pólya, o modelo ARTE foi utilizado com um grupo de 48 alunos. Os resultados, analisados por meio de testes não paramétricos devido à distribuição não normal das pontuações, revelaram melhorias significativas em todas as fases do método Pólya após a intervenção. Deduz-se que o modelo ARTE tem um impacto positivo no desenvolvimento da competência de resolução de problemas.

Palavras-chave: Competência em Resolução de Problemas, Modelo ARTE, Ciclo de Kolb, Método de Pólya, Google Classroom.

INTRODUCCIÓN

La destreza para resolver problemas, entendida como la capacidad para enfrentar y superar dificultades intelectuales sin soluciones evidentes ni inmediatas (OCDE, 2014), es esencial en el ámbito educativo. Las plataformas virtuales, además de facilitar tareas como la búsqueda de información y la redacción de apuntes, tienen el potencial de transformar el proceso de enseñanza-aprendizaje en una herramienta didáctica eficaz, adaptándose a las metodologías y características de los estudiantes (Marqués, 2012). Sin embargo, a nivel global, se observa que esta habilidad fundamental presenta serias dificultades en su aplicación a través de diversos niveles educativos.

330

La evaluación PISA 2012 reveló un desempeño preocupante en América Latina, incluyendo Perú, donde los resultados en competencias matemáticas fueron desalentadores. Colombia, Chile, Argentina y México mostraron porcentajes significativos de estudiantes en el nivel más bajo en competencias matemáticas. El Perú, en particular, se ubicó por debajo del promedio regional y presentó un bajo rendimiento en matemática durante varias ediciones de la prueba PISA, aunque se observó una ligera mejora en los años siguientes.

El problema se extiende a la educación básica y superior, donde las deficiencias en competencias matemáticas persisten. En la Evaluación Censal de Estudiantes (ECE), a pesar de un leve incremento en el rendimiento satisfactorio, los resultados siguen siendo insuficientes, con una persistente necesidad de reforzar los aprendizajes básicos. En las instituciones de educación superior, los estudiantes continúan enfrentando grandes dificultades en asignaturas fundamentales como Matemática Básica y Cálculo I, con tasas alarmantes de desaprobación.

Para el logro de la resolución de problemas, es necesaria una planificación estructurada y correctamente elaborada por el docente, tal que oriente el proceso de enseñanza y permita a los estudiantes el desarrollo de sus competencias. Según (UNESCO, 2022, p. 16) los docentes de calidad, se enfrentan a grandes desafíos, entre los cuales, no solo deben de conseguir saberes matemáticos, sino que también deben poner énfasis en los conocimientos pedagógicos, son estos los que les permiten organizar y planificar sus clases, estas formas de conocimiento deben de obligatoriamente integrarse en su labor docente.

Estos desafíos se relacionan a diversos tópicos, incluyendo metodologías de enseñanza tradicionales, falta de adaptación a nuevas tendencias educativas y el escaso uso de tecnologías. La metodología empleada por los docentes a menudo no promueve adecuadamente la competencia en resolución de problemas, lo que lleva a la necesidad de una revisión y mejora en las estrategias pedagógicas.

La pandemia del Coronavirus entre los años 2020 y 2021, obligo a la paralización presencial de las labores educativas en todos los niveles en el Perú, la mayoría de los estudiantes no estaba preparado para tan grande cambio, las instituciones de nivel superior no fueron la excepción y tanto estudiantes como docentes tuvieron que confinarse en sus hogares para desarrollar desde allí las sesiones de clase en forma sincrónica o asincrónica, teniendo como prioridad que las clases no debían detenerse, de esa forma se hizo uso de las plataformas virtuales entre ellas Blackboard, Moodle, Classroom etc. para el desarrollo de las sesiones de clase, lo que se denominó ‘enseñanza remota de emergencia’ (Pardo y Cobo, 2020)

331

Por todo lo mencionado este estudio se propone explorar la efectividad de una propuesta de sesión de aprendizaje basada en el ciclo de Kolb (ARTE: Actuar, Reflexionar, Teorizar y Experimentar), complementada con el método de Pólya para la resolución de problemas matemáticos viabilizada a través de la plataforma Classroom. La pregunta central es si el uso de este modelo, implementado a través de la plataforma Classroom, puede contribuir significativamente al desarrollo de la competencia en resolución de problemas entre los estudiantes de la asignatura de Matemática Básica

MÉTODO

El estudio realizado, presenta un enfoque cuantitativo, porque la variable se midió haciendo uso de métodos estadísticos y estableciendo conclusiones respecto a las hipótesis planteadas (Hernández, Fernández, y Baptista, 2014). Es una investigación de tipo aplicada y nivel experimental. Dado que el estudio se desarrolló en tiempos de pandemia, las clases de la asignatura de Matemática Básica fueron sincrónicas, apoyadas por el Google Classroom que permitió establecer cercanía con los estudiantes asimismo el desarrollo planificado de las sesiones de aprendizaje y un aula virtual donde se colocaban periódicamente los materiales a trabajar. El objetivo del estudio fue verificar que la propuesta de sesión de aprendizaje ARTE, sustentada en el ciclo de Kolb y método Polya es efectiva en el logro de la competencia resolución de problemas en estudiantes de la asignatura de Matemática Básica. Las variables del estudio son: Uso del modelo Arte usando Classroom (Variable Independiente) y Competencia Matemática Resolución de Problemas (Variable Dependiente), la misma que posee cuatro dimensiones: Comprensión del problema, Elaboración de un plan para la solución, Ejecución del Plan y Evaluación de la solución, cada una de las dimensiones será medida a través del cuestionario que se aplicará.

332

La población estuvo conformada por todos los estudiantes del primer ciclo de las diferentes escuelas profesionales que pertenecen a la Facultad de Ciencias Matemáticas de la Universidad Nacional Mayor de San Marcos, la conforman las escuelas de Matemática, Estadística, Computación Científica e Investigación Operativa. El tamaño de muestra fue de 48 estudiantes, se determinó por conveniencia, la cual se define como una técnica en donde los elementos se seleccionan por su accesibilidad o disponibilidad para el investigador. (Hernández, Fernández, y Baptista, 2014). La muestra tuvo los siguientes criterios de selección: a) Que sean estudiantes de la Facultad de Ciencias Matemáticas de la Universidad Nacional Mayor de San Marcos de la escuela profesional de Investigación Operativa b) Que tengan matricula regular en el semestre 2021-II en la asignatura de Matemática Básica c) Que sean ingresantes o repitentes por una sola vez de la asignatura de Matemática Básica dado que los estudiantes repitentes con 2 o más veces se les asigna un tutor académico.

Las técnicas en investigación son procedimientos específicos que se utilizan en determinadas áreas de la ciencia para la obtención de datos. Asimismo los instrumentos se definen como herramientas que forma parte de una técnica de recolección de datos. Puede darse como una guía, un manual, un aparato, una prueba, un cuestionario o un test. (Sánchez, Reyes, y Mejía, 2018)

La encuesta es una técnica de investigación que consiste en una interrogación verbal o escrita que se realiza a las personas con el fin de obtener determinada información necesaria para una investigación (Chávez-Moreno et al., 2023)

En la investigación, la técnica aplicada fue la encuesta y el instrumento fue un cuestionario con 5 preguntas cerradas en la forma de prueba de rendimiento de resolución de problemas que fue administrado de forma virtual. Este cuestionario fue validado en el contenido por juicio de expertos por 8 docentes que poseen el grado de magister y que ejercen la docencia universitaria en asignaturas de matemáticas. El instrumento fue evaluado en las dimensiones de: a) Claridad b) Relevancia c) Pertinencia d) Suficiencia. Con las observaciones realizadas por los expertos se corrigió el cuestionario

La confiabilidad del instrumento se midió a través del coeficiente de Kudder Richardson (KR-20) al ser trabajado con escala dicotómica. El valor del KR-20 fue de 0.76, según Nunnally (1987) el valor es adecuado para el estudio ya que supera el valor esperado al ser superior a 0.70.

En el estudio se realizó de forma continua y progresiva por cada sesión de clase, se verificó el avance de los estudiantes acompañado del uso de la plataforma; las evaluaciones teóricas en las semanas 4 y 12 sirvieron para medir resultados iniciales y de avance del curso. El Pre test se aplicó en la primera semana de clase para obtener información inicial de cómo se encuentra la competencia resolución de problemas y en la semana 16 se aplicó la prueba final con la cual se obtuvieron los resultados definitivos para realizar la comparación entre el pre y post test. Los Test sirvieron para comprobar el progreso de la resolución de problemas en matemáticas. (Sánchez et al., 2018)

333

Se aplicó la prueba de normalidad de Shapiro Wilk por ser el tamaño de muestra inferior a 50 datos (n=48), al no presentar normalidad se debió utilizar un test no paramétrico, el test de Wilcoxon para comparar si existe variación entre las medianas es la prueba ideal para la investigación realizada. Todos los resultados fueron procesados empleando el software estadístico SPSS versión 25.

RESULTADOS

La aplicación del Pre Test en la semana uno y el Post Test en la semana 16 empleando Classroom tuvieron las siguientes calificaciones medidas en escala vigesimal de 0 a 20.

Tabla 1. Media del Pre y Post Test

Estadísticos descriptivos
	N	Media	Desv. Desviación	Mínimo	Máximo
Pre Test	48	8.188	2.5320	4.0	13.0
Post Test	48	14.021	2.4188	8.0	18.0

Tal como se observa en la tabla 1, se evidencia un incremento de la media entre el Pre Test de 8.188 al Post Test de 14.021 después de la aplicación de las 16 sesiones de aprendizaje con el modelo ARTE, considerando las categorías de los niveles de logro según MINEDU (Ministerio de Educación del Perú) establecidas según: [0 – 10]: Inicio; [11-13]: Proceso; [14-17]: Esperado y [18-20]: Destacado, obtendríamos los siguientes resultados categorizados.

Tabla 2. Frecuencias porcentuales del Pre Test

PRE_TEST
		Frecuencia	Porcentaje	Porcentaje válido	Porcentaje acumulado
	Inicio	37	77.1	77.1	77.1
	Proceso	11	22.9	22.9	100.0
	Total	48	100.0	100.0

En el Pre Test, según la Tabla 2, las calificaciones determinan solo dos niveles de logro, en Inicio y Proceso, un 77.1% de ellos se encuentra en el nivel de Inicio mientras que solo el 22.9% se ubican en el nivel de Proceso

334

Tabla 3. Frecuencias porcentuales del Post Test

POST_TEST
		Frecuencia	Porcentaje	Porcentaje válido	Porcentaje acumulado
	Inicio	5	10.4	10.4	10.4
	Proceso	15	31.3	31.3	41.7
	Esperado	27	56.3	56.3	97.9
	Destacado	1	2.1	2.1	100.0
	Total	48	100.0	100.0

Después de aplicar las sesiones de aprendizaje con el modelo ARTE, según Tabla 3, las calificaciones se distribuyen en los 4 niveles de logro, reduciendo significativamente el nivel de Inicio con un 10.4%, además aparecen los niveles más altos de desempeño, como el nivel Esperado con un 56.3% y el nivel Destacado con un 2.1%.

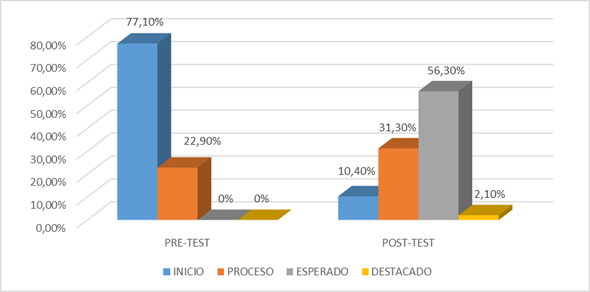Figura 1. Calificaciones en el Pre y Post Test y ubicación según nivel de logro

La figura 1, muestra un incremento significativo entre las calificaciones del Pre y Post Test, verificados en la aparición de los niveles Esperado y Destacado.

Posteriormente, se aplicó el test estadístico de Shapiro-Wilk para verificar la normalidad de los datos. El objetivo de esta prueba es determinar si los datos establecen una distribución normal, a partir de esto se considerará la aplicación de pruebas paramétricas o no paramétricas para el estudio.

Contrastación de Hipótesis

335

Tabla 4. Prueba de distribución de normalidad

	Pre Test			Post Test
Dimensiones		Estadístico	Sig.	Estadístico	Sig.
Comprensión del problema		.809	.000	.636	.000
Elaboración de un plan		.874	.000	.754	.000
Ejecución del plan		.858	.000	.844	.000
Evaluación del plan		.635	.000	.867	.000

Al analizar los resultados del p valor en el Pre Test y Post Test (Tabla 4), se observa que p=.000, en las cuatro dimensiones. Por lo tanto, se concluye que los datos no siguen una distribución normal. Debido a esta razón, se debe aplicar estadística no paramétrica.

Por la naturaleza de la investigación y la distribución no normal de los datos, el test de Wilcoxon para comparación de las medianas de dos muestras relacionadas es el método adecuado para su aplicación.

Prueba de Wilcoxon para la hipótesis general

H₀: No hay diferencia significativa entre la mediana de las calificaciones del pre test y post test aplicando el modelo ARTE empleando Classroom en el logro de la competencia resolución de problemas en los estudiantes del curso de Matemática Básica de una Universidad de Lima.

H₁: Hay diferencia significativa entre la mediana de las calificaciones del pre test y post test aplicando el modelo ARTE empleando Classroom en el logro de la competencia resolución de problemas en los estudiantes del curso de Matemática Básica.

Tabla 5. Test de Rangos de Wilcoxon

Rangos
		N	Rango promedio	Suma de rangos
Post Test – Pre Test	Rangos negativos	0^a	.00	.00
	Rangos positivos	46^b	23.50	1081.00
	Empates	2^c
	Total	48

336

El test de Rangos de Wilcoxon presentada en la Tabla 5, nos muestra que ningún estudiante en el Post Test obtuvo una calificación inferior a la del Pre Test, que 46 estudiantes obtuvieron calificaciones en el Post Test superiores a la del Pre Test y que solo 2 de ellos obtuvieron iguales calificaciones en el Post Test y el Pre Test, lo que nos muestra que existe un incremento en las calificaciones después de haber aplicado las sesiones de aprendizaje con el modelo ARTE.

Tabla 6. Prueba de Wilcoxon

Estadísticos de prueba
	POST TEST - PRE TEST
Z	-5.923^b
Sig. asintótica(bilateral)	.000

En la Tabla 6, según la prueba de Wilcoxon, se observa que el valor de la significancia p valor= .000 al ser inferior a .05, se puede rechazar la Hipótesis nula y se acepta la Hipótesis alterna, concluyendo que existe evidencia significativa para sustentar que la aplicación de las sesiones de aprendizaje en base al modelo ARTE contribuye en el logro de la competencia resolución de problemas al existir un cambio entre las calificaciones del Pre Test y Post Test.

Análisis descriptivo de la hipótesis especifica 1

Tabla 7. Media de la dimensión 1 del Pre y Post Test

Estadísticos descriptivos
	N	Media	Desv. Desviación	Mínimo	Máximo
Dimensión 1-Pre	48	3.94	.727	3	5
Dimensión 1-Post	48	4.52	.505	4	5

En la Tabla 7, se observa un incremento de la media de las calificaciones entre el Pre Test de 3.94 al Post Test de 4.52, asimismo el mínimo de puntaje obtenido en el Pre Test fue de 3 puntos y el mínimo del Post Test se incrementó a 4 puntos en la dimensión Comprensión del Problema en los estudiantes del curso de Matemática Básica.

Figura 2. 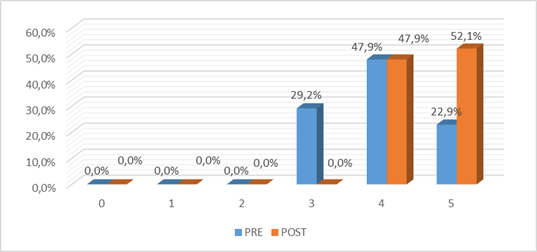Comprensión del problema en pre test y del post test

337

En la figura 2, se muestra que de 5 puntos posibles de obtener en la dimensión Comprensión del problema, en el Pre Test el 29.3% de alumnos obtuvieron 3 puntos, 47.9% 4 puntos, y sólo el 22.9% 5 puntos; entre tanto, posterior a la aplicación del Post Test usando el modelo de sesión de aprendizaje ARTE, el 47.9% obtuvieron 4 puntos y el 52.1%, 5 puntos, mostrándose un incremento evidente y significativo en las calificaciones.

Prueba de Wilcoxon para la hipótesis especifica 1

H₀: No hay diferencia significativa entre la mediana de las calificaciones del pre test y post test aplicando el modelo ARTE empleando Classroom en la comprensión del problema en los estudiantes del curso de Matemática Básica.

H₁: Hay diferencia significativa entre la mediana de las calificaciones del pre test y post test aplicando el modelo ARTE empleando Classroom en la comprensión del problema en lo estudiantes del curso de Matemática Básica.

Tabla 8. Test de Rangos de Wilcoxon

Rangos
		N	Rango promedio	Suma de rangos
Dimensión 1 -Post – Dimensión 1-Pre	Rangos negativos	2^a	11.50	23.00
	Rangos positivos	25^b	14.20	355.00
	Empates	21^c
	Total	48

Del test de Rangos de Wilcoxon mostrada en la Tabla 8, se observa que de los 48 estudiantes que participaron en las sesiones de aprendizaje con el modelo ARTE, 2 de ellos obtuvieron en el Post Test una calificación inferior a la del Pre Test, 25 obtuvieron calificaciones superiores en el Post Test y 21 obtuvieron iguales calificaciones en el Post Test y Pre Test en la dimensión Comprensión del Problema.

Tabla 9. Prueba de Wilcoxon

Estadísticos de prueba
	Dimensión 1-Post – Dimensión 1-Pre
Z	-4.274^b
Sig. asintótica(bilateral)	.000

338

En la Tabla 9, según la Prueba de Wilcoxon, el valor de la significancia p valor= .000 al ser inferior a .05, se rechaza la Hipótesis nula y se acepta la Hipótesis alterna, concluyendo que existe evidencia significativa para sustentar que la aplicación de las sesiones de aprendizaje en base al modelo ARTE contribuye con la Comprensión del Problema al existir un cambio entre las calificaciones del Pre Test y Post Test.

Análisis descriptivo de la hipótesis específica 2

Tabla 10. Media de la dimensión 2 del Pre y Post Test

Estadísticos descriptivos
	N	Media	Desv. Desviación	Mínimo	Máximo
Dimensión 2-Pre	48	2.67	.996	0	4
Dimensión 2- Post	48	4.21	.651	2	5

Según la tabla 10, se observa un incremento de la media de las calificaciones entre el Pre Test de 2.67 al Post Test de 4.21, asimismo, el mínimo de puntaje obtenido en el Pre Test fue de 0 puntos y el mínimo del Post Test se incrementó a 2 puntos en la dimensión Elaboración del Plan para la solución del problema en los estudiantes de Matemática Básica.

Figura 3. Elaboración de un plan en Pre Test y Post Test.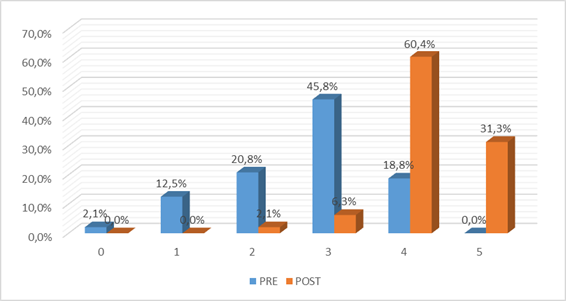

339

En la figura 3, se observa que de 5 puntos posibles de obtener en la dimensión Elaboración de un plan para la solución del problema, en el Pre Test el 20.8% de los estudiantes obtuvieron 2 puntos, 45.8% 3 puntos, 18.8% 4 puntos y ninguno obtuvo los 5 puntos; en tanto, posterior a la aplicación del Post Test usando el modelo de sesión de aprendizaje ARTE, el 6.3% obtuvo 3 puntos, el 60.4% 4 puntos y el 31.3% los 5 puntos, mostrándose un incremento evidente y significativo en las calificaciones.

Prueba de Wilcoxon para la hipótesis específica 2

H₀: No hay diferencia significativa entre la mediana de las calificaciones del pre test y post test aplicando el modelo ARTE empleando Classroom en la elaboración del plan para la solución del problema en los estudiantes del curso de Matemática Básica.

H₁: Hay diferencia significativa entre la mediana de las calificaciones del pre test y post test aplicando el modelo ARTE empleando Classroom en la elaboración del plan para la solución del problema en estudiantes de Matemática Básica.

Tabla 11. Test de Rangos de Wilcoxon

Rangos
		N	Rango promedio	Suma de rangos
Dimensión 2-Post –Dimensión 2-Pre	Rangos negativos	0^a	.00	.00
	Rangos positivos	44^b	22.50	990.00
	Empates	4^c
	Total	48

Del test de Rangos de Wilcoxon mostrada en la Tabla 11, se observa que de los 48 estudiantes quienes se sometieron a la aplicación de las sesiones de aprendizaje con el modelo ARTE, ninguno de ellos obtuvo en el Post Test una calificación inferior a la del Pre Test, 44 estudiantes obtuvieron calificaciones en el Post Test superiores a la del Pre Test y 4 de ellos obtuvieron iguales calificaciones tanto en el Post Test como el Pre Test en la Dimensión Elaboración de un plan para la solución del problema.

Tabla 12. Prueba de Wilcoxon

Estadísticos de prueba
	Dimensión 2-Post - Dimensión 2-Pre
Z	-5.917^b
Sig. asintótica(bilateral)	.000

340

En la Tabla 12, según la prueba de Wilcoxon, se observa que el valor de la significancia p valor= .000 al ser inferior a .05, permite rechazar la Hipótesis nula y se aceptar la Hipótesis alterna, concluyendo que existe evidencia significativa para sustentar que la aplicación de las sesiones de aprendizaje en base al modelo ARTE contribuye con la Elaboración de un plan para la solución del problema al existir un cambio entre las calificaciones del Pre Test y Post Test.

DISCUSIÓN

Hoy en día, la competencia matemática en la resolución de problemas es de suma importancia en las instituciones educativas a todos los niveles. Se reconoce como un pilar esencial que todo estudiante del siglo XXI debe adquirir y se considera uno de los tres ejes principales, según la OCDE (2014). De igual manera, en la educación superior, Córdova et al. (2017) la consideran una parte fundamental del desarrollo integral de la competencia matemática.

La hipótesis general de la investigación plantea que la implementación del modelo ARTE utilizando Classroom favorece el desarrollo de la competencia matemática de "resolución de problemas". Los resultados obtenidos respaldan esta hipótesis, lo cual se verificó a través del procesamiento y análisis de datos, permitiéndonos inferir que ha habido una mejora significativa en dicha competencia. Basándonos en los resultados de las evaluaciones de los cuestionarios aplicados en el pre y post test, se puede concluir que la hipótesis ha sido confirmada.

Se debe mencionar que las sesiones de clase fueron desarrolladas mediante el uso de la plataforma Classroom y con apoyo de herramientas tecnológicas (TIC). Debido a la emergencia sanitaria por el Covid-19, las clases en el semestre 2021-II, fueron sincrónicas.

Los resultados obtenidos coinciden con los hallazgos de Ayala (2021), quien en su investigación afirmó que el método Pólya influye significativamente en las calificaciones del curso de matemáticas.

Del mismo modo, este estudio es similar a los aportes de Rodríguez (2019), quien concluyó que la implementación del método Pólya en las sesiones de clase mejoró de manera significativa el rendimiento académico de los estudiantes de la EPEF-UNMSM durante el semestre 2017-I. Esto se evidenció en los resultados del post test, donde en el nivel óptimo, el grupo control alcanzó un 25% de estudiantes, en contraste con el 54.3% del grupo experimental.

341

De manera similar, la investigación realizada coincide con los hallazgos de Ayasta (2017), quien determinó que, en el grupo experimental, el promedio de la evaluación en el pre test fue de 11,76, situándose en un nivel regular. Sin embargo, tras la aplicación del Método de Pólya, el promedio en el post test aumentó a 16,6, alcanzando un nivel bueno, lo que evidencia la influencia del Método de Pólya en la mejora de la resolución de sistemas de ecuaciones lineales en estudiantes de la Universidad Privada del Norte.

De manera similar, la investigación se alinea con los resultados de Soto et al. (2022), quienes determinaron que la enseñanza de los cursos con mayor índice de desaprobación en la Facultad de Ingeniería se vuelve más efectiva cuando se diseñan y planifican las sesiones de clase basadas en el ciclo de Kolb. La evidencia muestra que el índice de desaprobación en estas asignaturas disminuyó considerablemente tras la intervención, subrayando la importancia de construir material didáctico siguiendo las etapas del ciclo de aprendizaje de Kolb. Esto demuestra que es posible transformar la enseñanza, pasando de un enfoque centrado únicamente en la instrucción a uno que pone al estudiante en el centro del proceso educativo.

De manera similar, los datos coinciden con los hallazgos de Zegarra (2018), quien desarrolló una propuesta basada en el Método Pólya y su relación con el nivel de logro del aprendizaje matemático en los estudiantes de Estudios Generales de la Universidad de San Martín de Porres. Se concluyó que hay una fuerte correlación entre la aplicación del método Pólya y el nivel de logro en el aprendizaje matemático de estos estudiantes, recomendando que los docentes de la universidad sean capacitados en la implementación del método en todas las sesiones de la asignatura de matemáticas.

Por lo que se puede concluir que la hipótesis general es validada y al mismo tiempo se relaciona directamente con los hallazgos de Ayala (2021), Rodríguez (2019), Ayasta (2017), Soto et al., (2022) y Zegarra (2018). Se concluye que al aplicar sesiones de aprendizaje con el modelo ARTE, se contribuye al logro de la competencia resolución de problemas.

CONCLUSIONES

La teoría del aprendizaje experiencial de Kolb describe cómo el aprendizaje ocurre a través de un ciclo que incluye la experiencia directa, la reflexión, la conceptualización abstracta y la experimentación activa. Aunque cada individuo tiene una inclinación por ciertos estilos de aprendizaje dentro de este ciclo, el aprendizaje efectivo requiere atravesar completamente estas cuatro fases.

342

El método Pólya es una estrategia para la resolución de problemas que se divide en cuatro etapas clave: entender el problema, elaborar estrategias para solucionarlo, aplicar esas estrategias y, finalmente, comprobar si la solución es correcta y apropiada. Esta metodología promueve la creatividad, la adaptabilidad y el pensamiento crítico en la resolución de problemas matemáticos entre los estudiantes universitarios que participaron en el estudio.

El estudio realizado ha demostrado que el modelo de sesión de aprendizaje ARTE, basado en el ciclo de aprendizaje experiencial de Kolb y el método Pólya, ha sido efectivo para mejorar la competencia matemática en resolución de problemas. Esto se refleja en que 46 de los 48 estudiantes que conformaron la muestra obtuvieron calificaciones en el Post Test superiores a las del Pre Test. El modelo ARTE constituye una propuesta de planificación de clases que favorece el desarrollo de la competencia matemática en los estudiantes y ofrece a los docentes una alternativa para fortalecer sus habilidades pedagógicas, facilitando el proceso de enseñanza-aprendizaje.

El empleo del modelo ARTE ha mejorado la comprensión de los problemas, ya que los estudiantes pudieron identificar variables, reconocer datos y definir el objetivo a alcanzar. Esto permitió dirigir el trabajo de manera eficiente, evitando operaciones irrelevantes que no contribuyen a la solución del problema, subrayando así su importancia. Se determinó que, en la dimensión de Comprensión del problema, la media de las calificaciones en el Pre Test fue de 3.84 puntos, mientras que en el Post Test la media aumentó a 4.52 puntos. Además, 25 estudiantes lograron calificaciones más altas en el Post Test en comparación con el Pre Test, y 21 estudiantes obtuvieron calificaciones iguales en ambos. En cada sesión de aprendizaje, durante la fase de Teorizar, se promovió la comprensión del problema a través de la intervención del docente mediante exposiciones dialogadas.

343

La implementación del modelo ARTE ha sido clave en la elaboración de planes para resolver problemas. En esta etapa, los docentes deben promover el trabajo en equipo, permitiendo que los estudiantes tengan autonomía para desarrollar su propio plan de solución. A través de la interacción, los estudiantes muestran tolerancia y respeto por las opiniones de los demás. Además, se enfocan en identificar y reconocer qué operaciones, recursos, teoremas o aplicaciones similares pueden ser útiles para resolver el problema. Se ha determinado que, en la dimensión de Elaboración del plan para la solución del problema, la media de las calificaciones en el Pre Test fue de 2.67 puntos, mientras que en el Post Test la media aumentó a 4.21 puntos. Asimismo, 44 estudiantes obtuvieron calificaciones más altas en el Post Test en comparación con el Pre Test, y 4 estudiantes obtuvieron calificaciones iguales en ambos. En cada sesión de aprendizaje, durante la fase final de Teorizar, se incentivó la elaboración del plan para resolver el problema.

La aplicación del modelo ARTE ha mejorado la Ejecución del plan para resolver problemas. Los participantes presentan y llevan a cabo sus propuestas, justificando sus elecciones y verificando sus respuestas. Esto promueve el trabajo en equipo, la tolerancia ante posibles observaciones de sus compañeros y el apoyo mutuo entre los miembros del grupo. Se ha observado que, en la dimensión de Ejecución del plan para la solución del problema, la media de las calificaciones en el Pre Test era de 1.1 puntos, mientras que en el Post Test aumentó a 3.37 puntos. Además, 44 estudiantes lograron calificaciones superiores en el Post Test en comparación con el Pre Test, y 3 estudiantes obtuvieron calificaciones iguales en ambos test. En cada sesión de aprendizaje, durante la fase de experimentar, se incentivó la ejecución del plan para resolver el problema.

La implementación del modelo ARTE ha sido efectiva en la evaluación del plan para resolver problemas. En esta etapa final, se promovió que los estudiantes mejoraran sus propuestas de solución o presentaran nuevas maneras de abordar el problema. También se alentó a que utilizaran su plan como modelo para futuros problemas y a que propusieran un problema real en el que pudieran aplicar su solución. Se ha observado que, en la dimensión de evaluación del plan para la solución del problema, la media de las calificaciones en el Pre Test fue de 0.38 puntos, mientras que en el Post Test subió a 1.92 puntos. Además, 36 estudiantes obtuvieron calificaciones superiores en el Post Test comparado con el Pre Test, y 10 estudiantes mantuvieron calificaciones iguales en ambos test. Durante la fase final de experimentar, se promovió la evaluación del plan para resolver el problema.

REFERENCIAS

Ayala, M. (2021). Método polya en la resolución de problemas y su influencia en el aprendizaje de las matemáticas en estudiantes de una Universidad Pública de Lima, 2021 [Tesis de maestría, Universidad Cesar Vallejo].

Ayasta, P. (2017). El Método Polya y el nivel de logros en la resolución de Ecuaciones Lineales en la asignatura de Matemática Básica en la Universidad Privada del Norte [Tesis de maestría, Universidad Nacional de Educación].

Chávez Moreno, R., Apodaca-Lopéz, C., Lugo-Tapia, T., Ochoa-Barraza, P., y Félix-Ortiz, G. (2023). Manual de Terminología de Investigación. Ciencia Latina Revista Científica Multidisciplinar, 7(3), 2101-2135. https://doi.org/10.37811/cl_rcm.v7i3.6335

344

Córdova, N. (2017). En búsqueda de un sistema de formación de habilidades en matemáticas. INNOVA, 2(2), 84-94. http://orcid.org/0000-0003-2954-8152

Eichmann, B., Goldhammer, F., Greiff, S., Pucite, L., y Naumann, J. (2019). The role of planning in complex problem solving. Computers & Education(128), 1-12. https://doi.org/10.1016/j.compedu.2018.08.004

García, C., y Rincón de Castro, C. (2014). ¿Cómo secuenciar actividades de EpD siguiendo el metodo del Aprendizaje Experiencial o Ciclo de Kolb?. Proyecto EpD - FISC. https://epdccbb.wordpress.com/2014/04/28/proyecto-epd-fisc-de-cesar-garcia-rincon/

Gibbs, G. (2013). Learnig by Doing. Oxford Brookes University. https://thoughtsmostlyaboutlearning.files.wordpress.com/2015/12/learning-by-doing-graham-gibbs.pdf

Hernández, R., Fernández, C., y Baptista, P. (2010). Metodología de la Investigación, Mc Graw Hill.

Hernández-Morales, J., Castañeda, A., y González-Polo, R. (2019). La solución de un problema matemático no convencional por estudiantes universitarios. Revista Científica, 35(2), 201-215. https://doi.org/10.14483/23448350.14863

Kolb, D., y Kolb, A. (2005). Experiential Learning Theory. Academy of Management Learning & Education, 4(2), 193-212. https://doi.org/10.1007/978-1-4419-1428-6_227

Lerman, S. (2014). Encyclopedia of Mathematics Education. Problem Solving in Mathematics Education. Springer Reference.

Lester, F. (2013). Thoughts About Research On Mathematical Problem- Solving Instruction. The Mathematics Enthusiast, 10(1), 245-278. https://doi.org/10.54870/1551-3440.1267

Marqués, P. (2012). Impacto de las TIC en la educación : Funciones y limitaciones. 3 c TIC: cuadernos de desarrollo aplicados a las TIC, 2(1), 1-15. https://3ciencias.com/wp-content/uploads/2013/01/3C-TIC_31.pdf

Matienzo, R. (2020). Evolución de la teoría del aprendizaje significativo y su aplicación en la educación superior. Dialektika, 2(3), 17-26. https://journal.dialektika.org/ojs/index.php/logos/issue/view/3/3.pdf

MINEDU. (2016). Currículo Nacional de Educación Básica. MINEDU.

Montero, L., y Mahecha, J. (2020). Comprensión y resolución de problemas matemáticos desde la macroestructura del texto. Praxis&Saber, 11(26). https://doi.org/10.19053/22160159.v11.n26.2020.9862

Nunnally, J.C. (1987). Teoría psicométrica. Editorial Trillas.

OCDE. (2014). ¿Los jóvenes de 15 años son creativos a la hora de resolver problemas? OCDE. https://www.oecd.org/pisa/pisaproducts/pisainfocus/PISA-in-Focus-N38-(esp).pdf

345

Organización de las Naciones Unidas para la Educación, l. C. (2022). Mathematics for Action. https://unesdoc.unesco.org/ark:/48223/pf0000380883.locale=en.pdf

Pardo, H., y Cobo, C. (2020). Expandir la universidad más allá de la enseñanza remota de emergencia. OUTLIERS SCHOOL.

Pólya, G. (1945). How to solve it (3ra ed.). Stanford University. https://math.hawaii.edu/home/pdf/putnam/PolyaHowToSolveIt.pdf

Rianti, R., Saragih, S., y Zulkarnain, Z. (2020). Development of Mathematics Learning Tools in the Context of Riau Malay Culture to Improve Students Mathematical Problem Solving Ability. Journal of Educational Sciences, 4(1), 73-82. https://doi.org/10.31258/jes.4.1.p.73-82

Rodríguez, N. (2019). Aplicación del método Pólya en el desempeño académico de los estudiantes de la Escuela Profesional de Educación Física de la Universidad Nacional Mayor de San Marcos 2017-I [Tesis de maestría, Universidad Nacional Mayor de San Marcos].

Sánchez, H., Reyes, C., y Mejía, K. (2018). Manual de términos en investigación científica, tecnológica y humanística. Universidad Ricardo Palma.

Simamora, R., Saragih , S., y Hasratuddin . (2019). Improving Students’ Mathematical Problem Solving Ability and Self- Efficacy through Guided Discovery Learning in Local Culture Context. International Electronic Journal of Mathematics Education, 14(1), 61-72. https://doi.org/10.12973/iejme/3966

Soto, O., Leal, P., y Sánchez, A. (2022). Apredizaje Experiencial en Ingeniería: Una aplicación de ciclo de Kolb. Congreso Sochedi 2022, Temuco, Chile.

http://www.sochedi.cl/congresos/xxxiv-congreso-chileno-de-educacion-en-ingenieria/

Zegarra, R. (2018). El Método Polya y su relación con el nivel del logro del aprendizaje [Tesis de maestría, Universidad Nacional de Educación].